iorewsilk.blogg.se - Harmonic progression

Harmonic progression series#

If the terms of the arithmetic progression are a, a + d, a + 2d, a + 3d. The reciprocal of the terms of the arithmetic progression gives the harmonic progression. The harmonic progression can be said to be derived from arithmetic progression.

What Is the Difference Between Arithmetic Progression and Harmonic Progression? And the harmonic progression obtained from the arithmetic progression with a common difference of 'd' is 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d).1/(a + (n - 1)d). The geometric progression having a common difference or 'r' is a, ar, ar 2, ar 3. The harmonic progression is the reciprocal of the arithmetic progression, and each term of the arithmetic progression is obtained by adding a constant value to the successive terms, called the common difference. The geometric progression is obtained by multiplying each term with a constant term called the common ratio, to obtain the next term. What Is the Difference Between Geometric Progression and Harmonic Progression? What Is an Example of Harmonic Progression?Īn example of harmonic progression is 1/2, 1/5, 1/8, 1/11. The harmonic progression is an infinite series. Here a is the first term and d is a common difference. The harmonic progression is formed by taking the reciprocal of the terms of the arithmetic progression. The nth term of the harmonic progression is 1/(a + (n - 1)d). The formula for harmonic progression is the formula to find the nth term of the harmonic progression. The following topics would help in a better understanding of harmonic progression.įAQs on Harmonic Progression What Is Harmonic Progression Formula?

In the field of finance, the profit earning ratio is computed using the concept of the weighted harmonic mean of individual components.

In geometry, the radius of the incircle of a triangle is equal to one-third of the harmonic mean of the altitudes of the triangle.

Harmonic Mean of two terms a and b = \(\dfrac\)

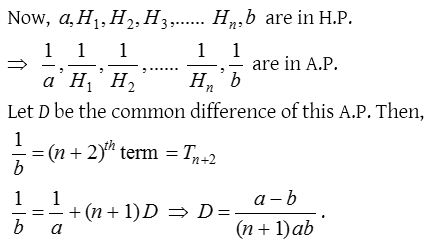
Harmonic progression series#

Harmonic Mean: In a harmonic progression, any term of the series is the harmonic mean of its neighboring terms. The nth term is useful to find any of the terms of the harmonic progression. term of the harmonic progression is the reciprocal of the sum of the first term and the (n - 1) times of the common difference. Nth term of a Harmonic Progression: It is the reciprocal of the nth term of the arithmetic progression. The following formulas are helpful for numerous calculations involving harmonic progression.